When you hear about formal methods in the context of software development, what do you picture in your mind? I would imagine a time consuming and possibly tedious process used in building mission-critical software, e.g. for a pacemaker or a space probe.

It may be something briefly visited during Computer Science courses at a college or university, quickly running through a few trivial examples. I have never actually had a chance to look into them before, so after reading the “loudly” titled “The Coming Software Apocalypse” in The Atlantic (interesting article by the way), it seemed intriguing.

Furthermore, interest has been elevated furthermore by the fact that Amazon Web Services team has had good success in using formal methods in their day to day work and they are continuing to push its adoption. (Use of Formal Methods at Amazon Web Services)

So the goal here is to learn enough about formal methods to be able to use them in at least one case on my own, whether at work or on a pet project. And just because there are a few books about TLA+ - that will be the focus of this experiment.

Why?

TLA+ is built to model algorithms and systems, to make sure they work as expected and catch any bugs lurking in them. It can be very helpful in finding subtle bugs in non-trivial algorithms or systems we create. When you write a specification, TLA+ Toolbox comes with a TLC Model checker that will check your specification and try to find issues in it. E.g. in one of the examples a bug TLC found took about 30 steps to reproduce. It also provides tools to explore certain properties of your system in question, e.g. what the system is allowed to do, or what the system eventually needs to do. This improves our confidence in systems we build.

With TLA+ we are working with a model of a system, which can work with and against us. With a model we can iterate faster, glossing over irrelevant details, exploring our ideas before we build out the final systems. But because we work with a model, we have to take great care in describing the model as to not gloss over critical behavior-altering details.

The other benefit we get is better understanding of systems we build, how they work and how they may fail. In order to write a spec it forces you to think about what needs to go right. To quote the AWS paper above, “we have found this rigorous “what needs to go right?” approach to be significantly less error prone than the ad hoc “what might go wrong?” approach.”

Learning about TLA+

To start with, Leslie Lamport produces a TLA+ Video Course. They will very clearly explain how TLA+ works, how to set up the Toolbox and get it running, run and write a few specifications as well, including parts of widely used algorithms, such as Paxos Commit (video version, paper).

Once up and running, mr. Lamport’s “Specifying systems” book provides an even more detailed look of TLA+. The book is comprehensive and can be a tough read, however it comprises of multiple parts and the first part “contains all that most engineers need to know about writing specifications” (83 pages).

And if you have checked out any of the specifications shared in the book and videos above, you may find that the way specifications are written is slightly different compared to the day-to-day programming languages one may use. Luckily, the Amazon paper mentions PlusCal, which is an accompanying language to TLA+ and feels more like a regular C-style programming language. They also report some engineers being more comfortable and productive with PlusCal, but still requiring extra flexibility provided by TLA+. You can learn more about PlusCal in Hillel Wayne’s online book Learning TLA.

Exploring tautologies

A tautology is defined as “[…] a formula which is “always true” — that is, it is true for every assignment of truth values to its simple components. You can think of a tautology as a rule of logic.” (ref). And in formal logic there are formulas which are equivalent, e.g. A -> B (A implies B) is equivalent to ~A \/ B (not A or B). So as a very basic starting point we can prove that with TLA+.

---------------------------- MODULE Tautologies ----------------------------
VARIABLES P, Q

F1(A, B) == A => B
F2(A, B) == ~A \/ B

FormulasEquivalent == F1(P, Q) <=> F2(P, Q)

Init ==
    /\ P \in BOOLEAN
    /\ Q \in BOOLEAN

Next ==
    /\ P' \in BOOLEAN
    /\ Q' \in BOOLEAN

Spec ==
    Init /\ [][Next]_<<P, Q>>
=============================================================================

The idea here is fairly simple: Let TLC pick arbitrary set of 2 boolean values, and we make sure that whatever those values are - results of F1 and F2 are always equivalent.

We declare 2 variables in our spec: P and Q. In the Init method we declare that both variables have some value from BOOLEAN set (which is equal to {TRUE, FALSE}). We don’t have to specify which particular values - TLC will pick them for us. Next is our loop step to mutate the values of P and Q. P' designates what the value of P will be after Next is executed. Again - we allow it to be any value from BOOLEAN set. This is important, because if we didn’t specify how exactly to mutate the value (or not change it) - TLC is free to pick an arbitrary value for it: NULL, "somestring", set {2, 5, 13}, etc. So up to this point we only allowed TLC to pick values of P and Q. They could be P = FALSE, Q = FALSE, P = FALSE, Q = TRUE, P = TRUE, Q = FALSE, P = TRUE, Q = TRUE.

We check our condition by configuring TLC to check if our invariant FormulasEquivalent holds. An invariant is a property that has to hold as the data mutates. In our case it’s “whatever P and Q values are, results of F1(P, Q) and F2(P, Q) should be equivalent”.

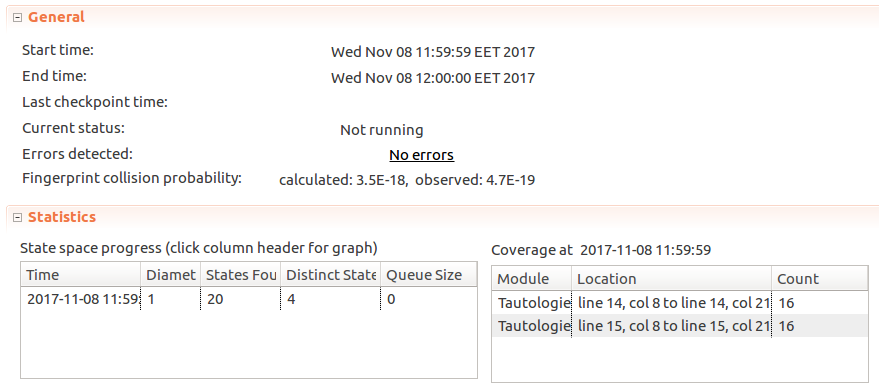
Once we run TLC, it reports that there were 4 distinct states (as we expected), and that there are no errors - our model worked as we expected.

Now, if we intentionally make a mistake and declare F2 as F2(A, B) == A \/ B by replacing ~A with A (removing negation), we can rerun the model and see what TLC finds:

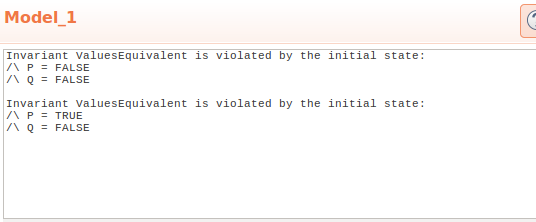
We see that TLA found two states where our invariant does not hold:

Invariant FormulasEquivalent is violated by the initial state:
/\ P = FALSE
/\ Q = FALSE

Invariant FormulasEquivalent is violated by the initial state:
/\ P = TRUE
/\ Q = FALSE

Which is exactly what we expected. Similarly we can check equivalence for ~(A /\ B) <=> (~A \/ ~B), P <=> (P \/ P), (P => Q) <=> (~Q => ~P), etc. Useful? Not very, but it gets us writing and checking some basic specs.

Closing thoughts

After running through the tutorial videos, first part of the “Specifying systems” book and “Learn TLA+” book I thought I had the grasp of it, but the air quickly ran out once I turned to attempting write specifications without external guidance. Perhaps specifying a sorting algorithm or solving a magic square was too much to quick and more practice is needed with simpler specifications. Finding an interesting yet achievable algorithm to specify is proving to be a challenge. So this part stops here with only the first trivial spec for proving equivalent logic formulas, and in the next part it may be interesting to try specifying a basic rate limiting algorithm.

In the meantime, running through TLA+ examples on Github helped better understand the types of algorithms TLA+ can specify and the way more complex specifications are written.